Publisher's description
AutoFEM Buckling Analysis is usefull in designing structures, operation of which involves a lasting impact on the intensity of various loads. With this module the user can obtain the safety margin for the so-called "Critical load" - load at which the design can be a significant leap inelastic deformation, often leading to its destruction or serious damage.
In the parameters of the problem of stability one can determine the number of forms of equilibrium states to be determined and other parameters of the calculation.
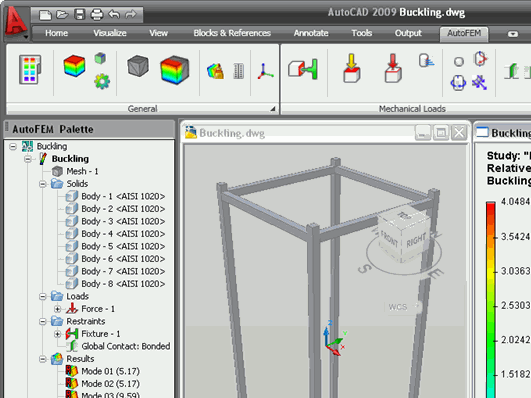
As result of buckling analysis, values of the coefficients of the critical loads at which there is loss of stability are obtained, as well as appropriate forms of instability.
The critical load factor - the estimated value of the coefficient whose product on applied load, gives the actual value of the critical load, causing the system to a new equilibrium. For example, the model is applied distributed force 1000 N. ratio of the critical load of the calculation results was 109.18. This means that the first form of stable equilibrium for this model has a critical load 109180 N.
The relative displacement (buckling mode) is a shape of the equilibrium steady state corresponding to a certain critical load. Forms of equilibrium states that are displayed in the window Postprocessor after the calculation represent the relative displacement. Analysing these forms you can draw conclusions about the nature of displacement in situations of instability. Knowing the expected equilibrium shape at a certain critical load, can, for example, to specify additional fastening or support in the field of design corresponding to the peak of this form of equilibrium, which would effectively change the mechanical properties of the product.
In the parameters of the problem of stability one can determine the number of forms of equilibrium states to be determined and other parameters of the calculation.
As result of buckling analysis, values of the coefficients of the critical loads at which there is loss of stability are obtained, as well as appropriate forms of instability.
The critical load factor - the estimated value of the coefficient whose product on applied load, gives the actual value of the critical load, causing the system to a new equilibrium. For example, the model is applied distributed force 1000 N. ratio of the critical load of the calculation results was 109.18. This means that the first form of stable equilibrium for this model has a critical load 109180 N.
The relative displacement (buckling mode) is a shape of the equilibrium steady state corresponding to a certain critical load. Forms of equilibrium states that are displayed in the window Postprocessor after the calculation represent the relative displacement. Analysing these forms you can draw conclusions about the nature of displacement in situations of instability. Knowing the expected equilibrium shape at a certain critical load, can, for example, to specify additional fastening or support in the field of design corresponding to the peak of this form of equilibrium, which would effectively change the mechanical properties of the product.


User comments